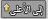مبرهنة الأعداد, le مبرهنة الأعداد الأولية هي نتيجة تهم كثافة توزيع عدد أولي. نعرف, لكل عدد حقيقي موجب x, العدد π(x) كعدد الأعداد الأولية الأصغر من x, مبرهمة الأعداد الأولية هي كالآتي :

من أجل قيم كبيرة x (ln (x) هو لوغاريثم نيبري ل x ; بالنسبة ل , انظر مفهوم لاندو).
, انظر مفهوم لاندو).
انظر الجدول :
احسن نتيجة تقريبية, هي تحسين للخطأ, معطاة بالصيغة التالية :

لقيم كبيرة ل x (Li هي الدالة لوغاريثم تكامل).
مبرهنة الأعداد الأولية تعطي معلومات حول توزيعية nرتبة عدد أولي
p(n)

كما يمكن استنتاج ان الاحتمال ليكون عدد طبيعي n عشوائي عدد أولي هو 1/ln(n).
مبرهنة الأعداد الأولية تم صياغتها حدسيا بواسطة عالم الرياضيات الألماني كوس في 1792 وكان عمره 15 سنة وبواسطة اندري ماري في
1798 وتمت البرهنة عليها بواسطة جاك هادمارد وشارل-جون في 1896.
البرهنة تستعين بطرق التحليل العقدي, وبخاصة دالة زيتا.
بسبب العلاقة الموجودة بين دالة زيتا وπ(x), فرضية ريمان ذات اعتبار مهم مبرهنة الأعداد : اذا تم البرهنة عليها, ستعطي احسن تنبؤ بنسبة الخطأ الناتجة عن مبرهنة الأعداد الأولية
هلغ فون كوخ في 1901 بين, بكيفية أدق, إذا كانت فرضية ريمان صحيحة, نسبة الخطأ تتحسن بالصيغة التالية :


من أجل قيم كبيرة x (ln (x) هو لوغاريثم نيبري ل x ; بالنسبة ل
 , انظر مفهوم لاندو).
, انظر مفهوم لاندو).انظر الجدول :
| 101 | 4 | 0 | 2 | 2,500 |
| 102 | 25 | 3 | 5 | 4,000 |
| 103 | 168 | 23 | 10 | 5,952 |
| 104 | 1 229 | 143 | 17 | 8,137 |
| 105 | 9 592 | 906 | 38 | 10,430 |
| 106 | 78 498 | 6 116 | 130 | 12,740 |
| 107 | 664 579 | 44 159 | 339 | 15,050 |
| 108 | 5 761 455 | 332 774 | 754 | 17,360 |
| 109 | 50 847 534 | 2 592 592 | 1 701 | 19,670 |
| 1010 | 455 052 511 | 20 758 029 | 3 104 | 21,980 |
| 1011 | 4 118 054 813 | 169 923 159 | 11 588 | 24,280 |
| 1012 | 37 607 912 018 | 1 416 705 193 | 38 263 | 26,590 |
| 1013 | 346 065 536 839 | 11 992 858 452 | 108 971 | 28,900 |
| 1014 | 3 204 941 750 802 | 102 838 308 636 | 314 890 | 31,200 |
| 1015 | 29 844 570 422 669 | 891 604 962 452 | 1 052 619 | 33,510 |
| 1016 | 279 238 341 033 925 | 7 804 289 844 392 | 3 214 632 | 35,810 |
| 4 ·1016 | 1 075 292 778 753 150 | 28 929 900 579 949 | 5 538 861 | 37,200 |

لقيم كبيرة ل x (Li هي الدالة لوغاريثم تكامل).
مبرهنة الأعداد الأولية تعطي معلومات حول توزيعية nرتبة عدد أولي
p(n)

كما يمكن استنتاج ان الاحتمال ليكون عدد طبيعي n عشوائي عدد أولي هو 1/ln(n).
مبرهنة الأعداد الأولية تم صياغتها حدسيا بواسطة عالم الرياضيات الألماني كوس في 1792 وكان عمره 15 سنة وبواسطة اندري ماري في
1798 وتمت البرهنة عليها بواسطة جاك هادمارد وشارل-جون في 1896.
البرهنة تستعين بطرق التحليل العقدي, وبخاصة دالة زيتا.
بسبب العلاقة الموجودة بين دالة زيتا وπ(x), فرضية ريمان ذات اعتبار مهم مبرهنة الأعداد : اذا تم البرهنة عليها, ستعطي احسن تنبؤ بنسبة الخطأ الناتجة عن مبرهنة الأعداد الأولية
هلغ فون كوخ في 1901 بين, بكيفية أدق, إذا كانت فرضية ريمان صحيحة, نسبة الخطأ تتحسن بالصيغة التالية :