تبسيط المعادلات والتراتب في العمليات الحسابية
عند قيامك بتبسيط مقدار رياضي ، قد تعتقد أن اتباع التسلسل الصحيح في إجراء العمليات الحسابية هو مسألة بديهية وسهلة !
ولكن مهلاً !!
دعنا ننظر معاً إلى بعض الأمثلة التي قد تربكك وتوقعك في أخطاء لم تكن تعتقد أنك ستقترفها .
 |
بينما قام خليل بتبسيط ذات العبارة العددية (5 + 4 × 3) على صورة المقدار العددي = 17
تُرى أيهما أتبع الخطوات الحسابية بتسلسل صحيح ؟؟
أحمد | خليل |
| 5 + 4 × 3 = (5 + 4) × 3 = 9 × 3 = 27 | 5 + 4 × 3 = 5 + (4 × 3) = 5 + 12 = 17 |
 |
| (8 ÷ 2) × (6 + 4) ؟! | 1) |  | (8 ÷ 2 × 6 + 4) |
| (8 ÷ 2) × 6 + 4 ؟! | 2) | ||
| 8 ÷ (2 × 6) + 4 ؟! | 3) | ||
| 8 ÷ 2 × (6 + 4) ؟! | 4) | ||
..... وهكذا |
لقد اتفق الرياضيون على اتباع ترتيب معين أو تسلسل محدد لإجراء العمليات الحسابية بحيث يكون معلوماً وواضحاً لكل دارس أو مُدرس التسلسل الصحيح للخطوات التي يجب اتباعها عند تبسيط المقادير الرياضية.
يُمكننا اختصار هذا التسلسل كما يلي :
الأقواس ( ) ، الأسس والجذور ، الضرب ، القسمة ، الجمع ، الطرح .
| رجوع | تبسيط المعادلات والتراتب في العمليات الحسابية ~ التسلسل في تنفيذ العمليات الحسابية |
بسيط المعادلات والتراتب في العمليات الحسابية
التسلسل في تنفيذ العمليات الحسابية
سنبدأ هنا ، التدرب على اتباع القواعد الأساسية عند إجراء العمليات الحسابية المختلفة بغرض تبسيط العبارة أو المعادلة الرياضية .
من الواضح أن المعادلات والمقادير الرياضية تتضمن عموماً إلى جانب الأعداد والمتغيرات (الحروف) الرموز الرياضية من مثل إشارات : الضرب × ، القسمة ÷ ، الجمع + ، الطرح - ، المساواة =
| [(5 س + 3 ÷ 4 ص × 2 – 7 +)] | <TABLE style="BORDER-COLLAPSE: collapse" id=table244 border=0 width="50%"> <TR> <td>(س = 1، </TD> <td>  </TD> </TD><td>)</TD></TR></TABLE> |
 |
وعند قيامنا بصياغة المعادلات والمقادير الرياضية المختلفة، نلجأ كثيراً، كما يقوم الرياضيون، باستخدام الأقواس ( ) لحصر بعض المعطيات العددية أو الجبرية داخلها بغرض التوضيح أو كجزء من عملية التبسيط الأولي للمعادلات والمقادير الطويلة والمعقدة .
[(5 + 7) × (6 – 5)] ، 5 س + 4 – (7 – 2)
وقد تصادفنا معادلات أو مقادير رياضية تتضمن متغيرات (حروف) أو أعدادٍ مرفوعة لأسٍُ أو قوة عددية ما أو أنها على صورة جذر.
 | ، | 35 | ، | س2 | ، |  | ، |  |
وهكذا يتضح لنا أهمية معرفة تسلسل واتباع القواعد الأساسية التالية، والموضوعة من قبل الرياضيين والمتعارف عليها عالمياً، عندما نبدأ بتبسيط أي مقدار رياضي أو عند قيامنا بمحاولة إيجاد حل لمعادلة ما.
 إبدأ بمعالجة كل مقدار رياضي أو كل طرف من أطراف المعادلة من اليمين إلى اليسار .
إبدأ بمعالجة كل مقدار رياضي أو كل طرف من أطراف المعادلة من اليمين إلى اليسار . نفذ العمليات الحسابية الواردة ضمن أقواس أولاً .
نفذ العمليات الحسابية الواردة ضمن أقواس أولاً . نفذ عمليات فك (تبسيط) الجذور والأسس .
نفذ عمليات فك (تبسيط) الجذور والأسس . بعد ذلك نفذ عمليات الضرب (من اليمين إلى اليسار) .
بعد ذلك نفذ عمليات الضرب (من اليمين إلى اليسار) . ثم نفذ عمليات القسمة (من اليمين إلى اليسار) .
ثم نفذ عمليات القسمة (من اليمين إلى اليسار) . وبعد ذلك نفذ عمليات الجمع والطرح (من اليمين إلى اليسار) .
وبعد ذلك نفذ عمليات الجمع والطرح (من اليمين إلى اليسار) .الأقواس ، القوى ، الضرب ، القسمة ، الجمع ، الطرح .
تبسيط المعادلات والتراتب في العمليات الحسابية
خاصية التبديل
خاصية التبديل
الخاصية التبديلية (تبادل الحدود)
الجمع: 3 + 2 = 2 + 3 وبالمثل س + ص = ص + س
الضرب: 3 × 4 = 4 × 3 وبالمثل ل × ع = ع × ل
تبديل الحدود لا يؤثر على الناتج.
الخاصية الترتيبية
الجمع: ( 2 + 3) + 4 = (2 + 4) + 3 = (3 + 4) + 2
وبالمثل (س + ص) + ع = (س + ع) + ص = (ص + ع) + س
الضرب: س (ص × ع) = ع (ص × س) = ص (ع × س)
إعادة ترتيب الحدود لا يؤثر على الناتج.
خاصية التوزيع (الخاصية التوزيعية)
الضرب يوزع على الجمع
2 (5 + 3) = 2 × 5 + 2 × 3
وبالمثل س (ص + ل) = س ص + س ل
إضافة أو طرح صفر من العبارة الرياضية
الجمع مع صفر لا يؤثر على الناتج.
5 – 0 = 5 وبالمثل س – 0 = س
الضرب في واحد والقسمة على واحد لا يؤثر على الناتج.
5 × 1 = 5 وبالمثل س × 1 = س
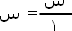 | وبالمثل |  |
5 – 5 = 0 وبالمثل 5 + ( - 5) = 0 وبالمثل س + (- س) = 0
| بشرط س ¹ 0 . |  | وبالمثل |  |
لقيمة العددية والمعادلة الجبرية
المعادلات (علاقات خاصة)
المعادلات (علاقات خاصة)
تساعدنا صياغة العلاقات الخاصة على شكل معادلة جبرية في حل الكثير من المسائل ، عندما نعرف القيم العددية للحروف (المتغيرات) ، المستخدمة في المعادلة .
لنأخذ العلاقة بين الطول و العرض
مثلاً العلاقة الخاصة بإيجاد مساحة المستطيل بدلالة أطوال أضلاعه .
لا بد أنك تعرف أن مساحة المستطيل = الطول × العرض وباستخدام الحروف نقول
لنأخذ العلاقة بين الطول و العرض
مثلاً العلاقة الخاصة بإيجاد مساحة المستطيل بدلالة أطوال أضلاعه .
لا بد أنك تعرف أن مساحة المستطيل = الطول × العرض وباستخدام الحروف نقول
م = ط × ع
حيث:
م = مساحة المستطيل بالسنتميتر المربع.
ط : طول المستطيل بالسنتميتر.
ع : عرض المستطيل بالسنتميتر.
تستطيع أن نجد مساحة المستطيل إذا علمت أن ط = 5 سم ، ع = 4 سم.
م = ط × ع
م = 5 سم × 4 سم
م = 20 سم2
وبالمثل :
أنت تعرف أن المسافة = السرعة × الزمن
وبالرموز م = س × ز
وبالرموز م = س × ز
حيث:
م : المسافة بالمتر.
س: السرعة بالمتر لكل ثانية.
ز : الزمن بالثانية.
تستطيع أن تعرف المسافة التي تقطعها سيارة تحركت مثلاً لمدة 20 ثانية وبسرعة ثابتة مقدارها 10متر لكل ثانية.
نقول م = س × ز
م = 10 متر / ثانية × 20 ثانية
م = 200 متر
المتغير والمُعامل والحد المطلق
عرفت أنّ الحدُّ الجبريُّ يتكوّن من حاصل ضربِ ثابتٍ بمتغير أو أكثر .
3س ، 7س ص ، 35 س3ص2ع ...
وعرفت أن العدد المضروب بمتغير أو أكثر في الحد الجبري يسمى المعامل .
ففي الحد الجبري 3س2 يكون معامل س2 هو (3) ، ومعامل س في الحد الجبري -2س هو (-2) ، ونقول أن (+5) هو معامل سفي الحد الجبري +5 س.
وعرفت أن المقدار الجبري يتكون من الحدود المفصولة عن بعضها بإشارة الجمع أو الطرح .
وهكذا فإن (3س2 – 2 س + 5 ) هو مقدار جبري فيه :
3 س2 حد جبري ، - 2 س حد جبري ، + 5 حد مطلق .
دَرست سابقاً أن العبارة الرياضية (5 + 5 + 5) يُمكن أن تُكتب اختصاراً على صورة (3 × 5) وبالمثل ، في علم الجبر فإن س + س + س = 3 × س (وتُكتب اختصاراً 3س).
ودَرست سابقاً أنَّ العدد 36 لا يعني أبداً (6 × 3) وإنما يعني (3) عشرات و 6 واحدات (آحاد) .
36 = (3) عشرات + (6) آحاد
ولكن في علم الجبر ، فإننا دائماً يجب أن نفهم أنَّ :
4 س تعني 4 × س
ونقول أن الأربعة (4) هي معامل المتغير (س)
أي أنها تخبرنا عن عدد مرات تكرار المتغير (س)
4 س = 4 × س = س + س + س + س
وبالمثل :
س ص تعني دائماً س × ص
ونقول (س) هي معامل للمتغير ص ، والعكس أيضاً (ص) هي معامل للمتغير س .
لنأخذ المقدار الجبري (3س × 4) ونَرى كيف يُمكننا فهمه .
3 س × 4 تعني 4 × 3 س
3 س + 3 س + 3 س + 3 س = 12 س
وكذلك 3 س × 4 = 3 × س × 4 = 3 × 4 × س = 12 × س = 12 س | وكذلك 3 س × 4 = 3 × س × 4 = 4 × س × 3 = 4 س × 3 |
3 س × 4 = 12 س = 4 س × 3
وبالمثل فإن المقدار (3 س × 4 ص) يعني
3 س × 4 ص = 12 س ص
= 4 س × 3 ص
المتغير ووحدة القياس الكمي
تَرمُز الحروف التي نستخدمها في المقادير الجبرية إلى أعدادٍ وليس إلى وحدات قياس لعددٍ من الأشياء .
فكما نقول (7) كيلو غرام ، (100) سم2 ، (15) متر ، (5) دراهم.
بالمثل نقول : (س) من الدنانير ، (ص) كيلوغرامات ، (ل) متر مربع ... وهكذا .
ونحنُ نستخدم الأحرف في الجبر، ليدل الواحد منها على مقدار عددي من نوعٍ واحد فقط .
فمثلاً قد تكون (س) ترمز إلى 7 كيلوغرامات أو قد تكون (ص) ترمز إلى 12 مسطرة ... وهكذا .
ولكنها ، أي (س) ، لا يمكن أن ترمز إلى نوعين مختلفين . فمثلاً (س) لا يمكن أن ترمز إلى 7 كيلوغرامات و12 مسطرة في آن واحد.
الحرف في الجبر (المتغير) يدل على نوع كمي واحد.
لنأخذ العبارة 6 + س = 20 كغم .
إنها تعني أن العدد 6 يدل على 6 كغم .
وأن (س) وحدتها الكيلوغرام وهي تدل على مقدار عددي.
6 + س = 20 كغم تعني لنا
6 كغم + (س) كغم = 20 كغم إذن س = 14 كغم
 |
لنأخذ المقدار الجبري (ص + 4) ولنفرض أن ص = 3 .
دَعنا الآن ندرس القيمة العددية للمقدار الجبري (ص + 4) على فرض أن ص = 3 .
 إذا كان المقدار (ص + 4) يُمثل وحدات قياس مساحةٍ ما ، فإن القيمة العددية لهذا المقدار الجبري هي:
إذا كان المقدار (ص + 4) يُمثل وحدات قياس مساحةٍ ما ، فإن القيمة العددية لهذا المقدار الجبري هي:(ص + 4) سم2 = (3) سم2 + 4 سم2
= 3 سم2 + 4 سم2 = 7 سم2
 وإذا كان المقدار (ص + 4) يمثل وحدات قياس مسافة طولية ما فإن القيمة العددية لهذا المقدار هي:
وإذا كان المقدار (ص + 4) يمثل وحدات قياس مسافة طولية ما فإن القيمة العددية لهذا المقدار هي: = 3 م + 4 م
= 7 م
 وإذا كان المقدار (ص + 4) يُمثل مبلغاً من النقود (دنانير مثلاً) ، فإن القيمة العددية لهذا المقدار هي:
وإذا كان المقدار (ص + 4) يُمثل مبلغاً من النقود (دنانير مثلاً) ، فإن القيمة العددية لهذا المقدار هي:(ص + 4) دينار = (ص) دينار + 4 دينار
= 3 دينار + 4 دينار = 7 دنانير